Web-версия учебного курса "Теория вероятностей"
Раздел 6. Типичные законы распределения и числовые характеристики случайных величин
Вид функций F(x), р(х), или перечисление р(хi) называют законом распределения случайной величины. Хотя можно представить себе бесконечное разнообразие случайных величин, законов распределения гораздо меньше. Во-первых, различные случайные величины могут иметь совершенно одинаковые законы распределения. Например: пусть y принимает всего 2 значения 1 и -1 с вероятностями 0.5; величина z = -y имеет точно такой же закон распределения.
Во-вторых, очень часто случайные величины имеют подобные законы распределения, т.е., например, р(х) для них выражается формулами одинакового вида, отличающимися только одной или несколькими постоянными. Эти постоянные называются параметрами распределения.
Хотя в принципе возможны самые разные законы распределения, здесь будут рассмотрены несколько наиболее типичных законов. Важно обратить внимание на условия, в которых они возникают, параметры и свойства этих распределений.
1 . Равномерное распределение
Так называют распределение случайной величины, которая может принимать любые значения в интервале (a,b), причем вероятность попадания ее в любой отрезок внутри (a,b) пропорциональна длине отрезка и не зависит от его положения, а вероятность значений вне (a,b) равна 0.
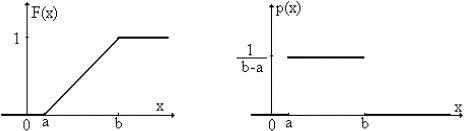
Рис 6.1 Функция и плотность равномерного распределения
Параметры распределения: a , b
2 . Нормальное распределение
Распределение с плотностью, описываемой формулой
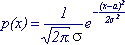 (6.1) (6.1)
называется нормальным. (Рисунок 6.2)
Параметры распределения: a , σ
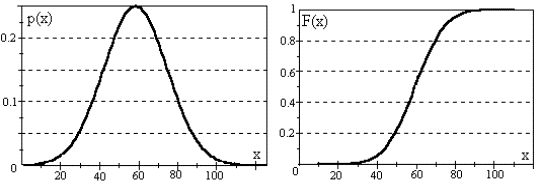
Рисунок 6.2 Типичный вид плотности и функции нормального распределения
3 . Распределение Бернулли
Если производится серия независимых испытаний, в каждом из который событие А может появиться с одинаковой вероятностью р, то число появлений события есть случайная величина, распределенная по закону Бернулли, или по биномиальному закону (другое название распределения).
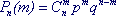 (6.2) (6.2)
Здесь n - число испытаний в серии, m - случайная величина (число появлений события А), Рn(m) - вероятность того, что А произойдет именно m раз, q = 1 - р (вероятность того, что А не появится в испытании).
Пример 1: Кость бросают 5 раз, какова вероятность того, что 6 очков выпадет дважды ?
n = 5, m = 2, p = 1/6, q = 5/6
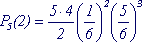
Параметры распределения: n , р
4 . Распределение Пуассона
Распределение Пуассона получается как предельный случай распределения Бернулли, если устремить р к нулю, а n к бесконечности, но так, чтобы их произведение оставалось постоянным: nр = а. Формально такой предельный переход приводит к формуле
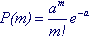 (6.3) (6.3)
Параметр распределения: a
Распределению Пуассона подчиняются очень многие случайные величины, встречающиеся в науке и практической жизни.
Пример 2: число вызовов, поступающих на станцию скорой помощи в течение часа.
Разобьем интервал времени Т (1 час) на малые интервалы dt, такие что вероятность поступления двух и более вызовов в течение dt пренебрежимо мала, а вероятность одного вызова р пропорциональна dt: р = μdt ;
будем рассматривать наблюдение в течение моментов dt как независимые испытания, число таких испытаний за время Т: n = T / dt;
если предполагать, что вероятности поступления вызовов не меняются в течение часа, то полное число вызовов подчиняется закону Бернулли с параметрами: n = T / dt, р = μdt . Устремив dt к нулю, получим, что n стремится к бесконечности, а произведение n×р остается постоянным: а = n×р = μТ.
Пример 3: число молекул идеального газа в некотором фиксированном объеме V.
Разобьем объем V на малые объемы dV такие, что вероятность нахождения двух и более молекул в dV пренебрежимо мала, а вероятность нахождения одной молекулы пропорциональна dV: р = μdV; будем рассматривать наблюдение каждого объемчика dV как независимое испытание, число таких испытаний n=V/dV; если предполагать, что вероятности нахождения молекулы в любом месте внутри V одинаковы, полное число молекул в объеме V подчиняется закону Бернулли с параметрами: n = V / dV, р = μdV. Устремив dV к нулю, получим, что n стремится к бесконечности, а произведение n×р остается постоянным: а = n×р =μV.
Числовые характеристики случайных величин
1 . Математическое ожидание (среднее значение)
Определение:
Математическим ожиданием называется
- для дискретной случайной величины: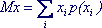 (6.4) (6.4)
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)
- для непрерывной случайной величины: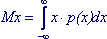 ; (6.5) ; (6.5)
Интеграл должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)
Свойства математического ожидания:
a . Если С - постоянная величина, то МС = С
b . МСх = СМх
c . Математическое ожидание суммы случайных величин всегда равно сумме их математических ожиданий: М(х+y) = Мх + Мy
d . Вводится понятие условного математического ожидания. Если случайная величина принимает свои значения хi с различными вероятностями p(xi/Hj) при разных условиях Hj, то условное математическое ожидание определяется
как 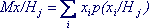 или или 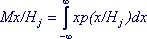 ; (6.6) ; (6.6)
Если известны вероятности событий Hj, может быть найдено полное
математическое ожидание: 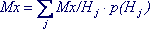 ; (6.7) ; (6.7)
Пример 4: Сколько раз в среднем надо бросать монету до первого выпадения герба ? Эту задачу можно решать "в лоб"
| xi | 1 2 3 ... k.. | |
| p(xi) : | 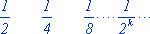 | 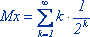 , , |
но эту сумму еще надо вычислить. Можно поступить проще, используя понятия условного и полного математического ожидания. Рассмотрим гипотезы Н1 - герб выпал в первый же раз, Н2 - в первый раз он не выпал. Очевидно, р(Н1) = р(Н2) = ½; Мx / Н1 = 1;
Мx / Н2 на 1 больше искомого полного матожидания, т.к. после первого бросания монеты ситуация не изменилась, но один раз она уже брошена. Используя формулу полного математического ожидания, имеем Мх = Мx / Н1×р(Н1) + Мx / Н2×р(Н2) = 1×0.5 + (Мх + 1)×0.5 , разрешая уравнение относительно Мх, получаем сразу Мх = 2 .
e . Если f(x) - есть функция случайной величины х, то определено понятие математического ожидания функции случайной величины:
- для дискретной случайной величины: 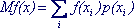 ; (6.8) ; (6.8)
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся.
-для непрерывной случайной величины: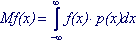 ; (6.9) ; (6.9)
Интеграл должен быть абсолютно сходящимся.
2 . Дисперсия случайной величины
Определение:
Дисперсией случайной величины х называется математическое ожидание квадрата отклонения значения величины от ее математического ожидания: Dx = M(x-Mx)2
- для дискретной случайной величины: 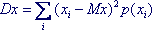 ; (6.10) ; (6.10)
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)
- для непрерывной случайной величины: 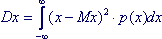 ; (6.11) ; (6.11)
Интеграл должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии)
Свойства дисперсии:
a . Если С - постоянная величина, то DС = 0
b . DСх = С2Dх
c . Дисперсия суммы случайных величин всегда равно сумме их дисперсий только, если эти величины независимы (определение независимых величин)
d . Для вычисления дисперсии удобно использовать формулу:
Dx = Mx2 - (Mx)2 (6.12)
Связь числовых характеристик
и параметров типичных распределений
| распределение | параметры | формула | Mx | Dx |
| равномерное | a , b | 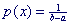 | (b+a) / 2 | (b-a)2 / 12 |
| нормальное | a , σ | 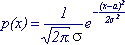 | a | σ2 |
| Бернулли | n , p | 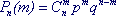 | np | npq |
| Пуассона | a | 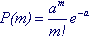 | a | a |
|

